Graphs Beyond the Hairball
Networks are usually drawn using a technique called node-link diagrams. While that works well for small graphs (the technical name for networks), it breaks down beyond a few dozen nodes. Better techniques exist, though these are currently focused on specific types of graphs or answer particular questions.
Node-Link Diagrams
When you think of a graph, you likely already think of a node-link diagram – unless you’re a mathematician. This technique is incredibly effective in communicating the basic idea of a network: there are nodes, typically shown as little dots or circles, and they’re connected by links, or edges in graph lingo. Even the difference between a directed and an undirected graph is obvious: little arrows mean that there’s a direction, no arrows means no direction. Lane Harrison gives a good overview on the Visual.ly blog. Carlos Scheidegger is also writing an interesting, if mathematical, series on graphs of the node-link variety.
These images are easy to understand even for people who have never seen such a diagram before, which is not something that can be said about many visualization techniques. Most people would also easily be able to figure out how to answer basic questions using such a diagram, like finding the person with the most friends (i.e., the node with the highest degree) or looking for highly connected groups that only have a small number of links between them (so-called cliques).
Hairballs
There is a catch, of course. The simplicity and beauty of node-link diagrams turns into clutter and confusion when the number of nodes and links gets too high: the dreaded hairball.

Many techniques have been developed to sort out the clutter: edge bundling, node filtering, edge lenses, many, many different layout algorithms, etc. But none of them provide a good, general solution to the underlying problem. The question also needs to be asked if the most obvious visual depiction is also the most effective. It may not be.
Matrix Methods
Matrix visualizations represent a very different approach. These techniques are based on the adjacency matrix, which defines which nodes in a graph are connected to which. Imagine a table with a row and a column for each node. The value in each cell of the matrix contains a value of 1 if there is a connection between the node in that row and that column, and 0 if not.

Matrix visualization techniques display that matrix rather than the node-link version of the graph. No more crossing lines and no more hairball. Seeing structures in such a visualization requires some training and some support from the visualization tool, but the advantage is that there are no more lines cluttering up the view. This illustration from Nathalie Henry and Jean-Daniel Fekete’s InfoVis 2006 paper MatrixExplorer: a Dual-Representation System to Explore Social Networks nicely shows how structures in the node-link diagram translate into the matrix view.

The rows and columns of the matrix can be rearranged, which represents one of the greatest strengths and weaknesses of matrix techniques at the same time: order matters. The patterns that are so obvious in the image above will be easily hidden by jumbling the order of the matrix. But given a good clustering and ordering algorithm, in particular one where the user can specify criteria and weights, a matrix view can show patterns very clearly.
Directed, Tree-Like Graphs: Node Quilts
A technique I found particularly fascinating at InfoVis 2011 was shown in a paper titled Developing and Evaluating Quilts for the Depiction of Large Layered Graphs by Juhee Bae and Ben Watson. Node quilts are designed specifically for directed, acyclic graphs (DAGs): graphs that have a hierarchical structure, where most links point from one layer to the next. This technique was originally designed for genealogical trees, but the version Bae and Watson studied allows links that point up as well (though they should be rare).
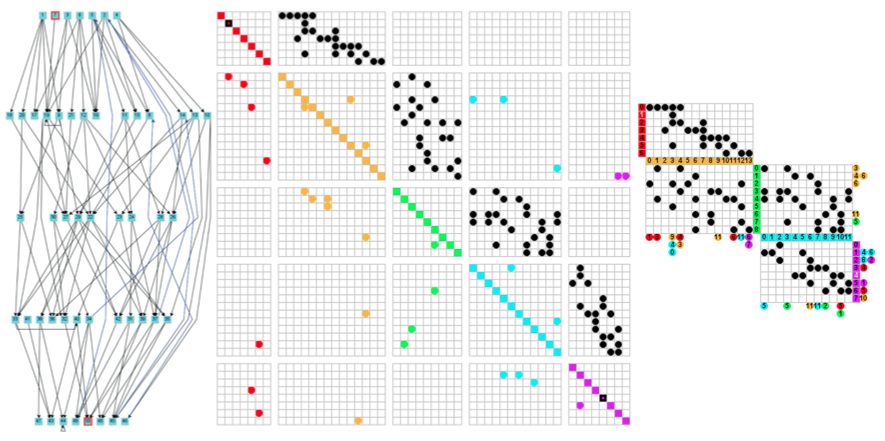
Node quilts cleverly exploit the fact that most of the action is in one half of the matrix by folding it to eliminate the parts that are (mostly) empty. The resulting visualization is much denser and also more informative: links that skip layers or that point back are shown outside the matrix itself.
This technique takes a bit of time and study to appreciate, but it extends the matrix visualization idea in a way that is very clever and useful – for particular tasks and data. But focus on particular types of questions is clearly a virtue given the issues with node-link diagrams in general. I also wonder how well the technique might work for undirected graphs, where the lower half of the adjacency matrix can be ignored because it is symmetrical. The focus on using quilts only for DAGs so far may be a bit more narrow than necessary.
What Are You Asking: PivotGraph
In many cases, it makes little sense to look at all the individual data items, while an appropriately aggregated view can provide much more useful information. This is the same idea as behind Parallel Sets and also almost all of the views in Tableau. In 2006, Martin Wattenberg published a paper on a technique he called PivotGraph that adapted the idea of aggregation for use with graphs. For the aggregation to work, there has to be data attached to the graph nodes, and it has to be partly categorical. This is typically the case when looking at rich data like email traffic, phone conversations, etc.
The PivotGraph has two interesting properties. First, it is very goal-directed: it requires the user to pick dimensions along which to aggregate, and which to use to lay out the graph. Second, it uses space in a very different way than node-link diagrams. While space in node-link diagrams is mostly there to avoid collisions between the nodes and clutter between the lines, it carries information in the case of the PivotGraph.

The example above shows the communication patterns between people in different departments (rows) and locations (columns). The width of the arrows represents the amount of communication going on (emails, etc.). This is aggregated information, not just along the edges but also in the nodes: each department and location consists of multiple people. What would have been a big hairball had all the individual items been shown has been turned into a much simpler image that answers a question.
Many questions that are asked about network data are of the same nature: How many people who have done A also do B? How do potential customers navigate the different elements on a website and where do they give up? What classes of products are bought together or in quick succession? etc.
The Graph Beyond the Graph
For a while now, people in visualization have talked about the graph without the graph, i.e., graph visualization without the hairballs. Networks are clearly important and challenging data, and it seems a bit myopic to only look at node-link visualization. Node quilts and the PivotGraph represent promising steps into a very different direction. While they require more work to understand and are more limited in what they can be used for, they are also much directed towards a goal than just showing all of the data. I think that this kind of thinking will lead us to much more interesting techniques in the future than trying to teach the old node-link diagram new tricks.

Comments (5)
Posting new comments was disabled in 2020.